Эффект бабочки
Когда трейдеры слышат о Волнах Эллиотта, они обычно наряду с этим слышат о соотношениях Фибоначчи. Так же верно и обратное. Когда обсуждаются соотношения Фибоначчи, то почти всегда в контексте Волн Эллиотта или измерения некоторого восстановления. Однако, я хотел бы предложить применение соотношения Фибоначчи к любой графической модели. В данной статье, будет представлена графическая модель, которая редко обсуждается среди трейдеров - Бабочка Гaртли.
Х. М. Гартли опубликовал книгу "Прибыль на фондовой бирже" в 1935г. В этой книге, он упоминает графическую модель, которую можно перепутать с известными Волнами Эллиотта. Есть сходства, но это - не те же самые модели. Там, где в Волнах Эллиотта используются числовые обозначения для импульсных волн и буквенные для коррекционных, модель Гартли использует только буквенное обозначение для разворотных или центральных точек в модели. Это только одно из различий, которое можно заметить сразу же, но есть и много других. Поэтому, трейдеры, которые использовали Волны Эллиотта, могут быть несколько смущены моделью Бабочки Гартли. Поэтому, может быть полезно принять материал, представленный здесь, таким как он есть, вместо того, чтобы сравнивать две модели между собой. Есть несколько разновидностей модели Бабочки, но в данной статье будет обсуждаться только одна разновидность.
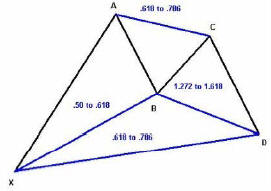
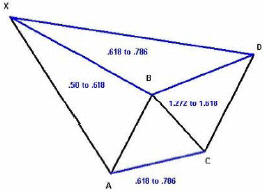
На вышеприведенной схеме мы видим общую модель Бабочки Гартли. На первый взгляд она может выглядеть очень странной. Однако, для начала я объясню модель и затем продемонстрирую графический пример. Черные линии в модели Бабочки представляют ценовые движения рыночного инструмента. Так, на схеме 1, мы можем видеть, что ценовое движение происходит из точки X до точки A. Затем, мы имеем нисходящее колебание до точки B, которая не выходит за пределы точки X. Это сопровождается движением до точки C, которая не превышает точку A. Наконец, Бабочка заканчивается в нисходящем колебании от точки C до точки D. Для целей обсуждения этой разновидности Бабочки Гартли, последовательные ценовые колебания от точки А до точки D находятся в пределах ценового диапазона, определенного точками X и A.
Синие линии на схеме представляют типичные соотношения Фибоначчи ценовых колебаний в пределах модели Бабочки. Ценовое колебание от точки А до точки B будет типично восстанавливать от 0.5 до 0.618 ценового диапазона, определенного движением от точки X до точки A. Ценовое восстановление, происходящее из точки B и заканчивающееся в точке C будет обычно заканчиваться в ценовом диапазоне между 0.618 и 0.786 от ценового колебания от точки А до точки B. Заключительное ценовое движение, которое происходит от точки C до точки D обычно имеет соотношение 1.272 - 1.618 к предшествующему колебанию между точками B и C. Ценовое колебание от точки C до точки D может также иметь соотношение Фибоначчи от 0.786 до 0.618 к ценовому движению от точки X до точки A.
Заключительное соотношение, которые обычно упоминается, заключается в равенстве ценового движения от точки C до точки D и ценового движения от точки А до точки B. Я также включаю соотношение Фибоначчи 1.618 для этой части структуры Бабочки. Следовательно, также следует искать ценовое колебание, которое происходит от точки C и заканчивается в точке D, чтобы оно равнялось 1.00 - 1.618 от длины колебания от точки А до точки B.
Если вы внимательно следили за только что представленными объяснениями модели Бабочки Гартли, то у вас может возникнуть вопрос, как строго модель должна выполнять указанные соотношения Фибоначчи. По моему мнению, соотношения Фибоначчи должны выполняться, по крайней мере, для двух последовательных ценовых колебаний. Это поможет нам математически подтвердить то, что мы видим на графике. Также, соотношения Фибоначчи для последнего ценового колебания от точки C до точки D должно иметь большее значение, чем другие соотношения Фибоначчи в модели Бабочки Гартли.
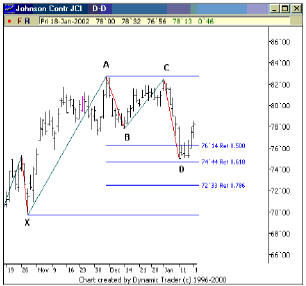
На представленном выше графике, мы имеем три синих горизонтальных линии, которые представляют уровни восстановления 0.50, 0.618 и 0.786 от полного ценового колебания от точки X до точки A. Помните, что мы используем соотношение 0.50 и 0.618 для движения от точки А до точки B. Также, мы используем уровни 0.618 и 0.786 для колебания от точки C до точки D. Таким образом, мы измеряем два различных ценовых колебания. Заметьте, что колебание от точки А до точки B не доходит очень близко до области восстановления 0.50 - 0.618. Это отличается от ценового движения между точкой C и точкой D, которое подходит очень близко к цели 0.618.
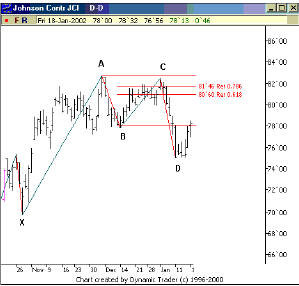
На данном графике, мы имеем уровни восстановления 0.786 и 0.618 ценового колебания от точки А до точки B. Обратите внимание, что мы имеем ценовое движение, которое способно превысить этот уровень 0.786 и закрыться выше. Однако, рынок неспособен поддержать пересечение этого уровня, и на следующий день закрывается ниже него.
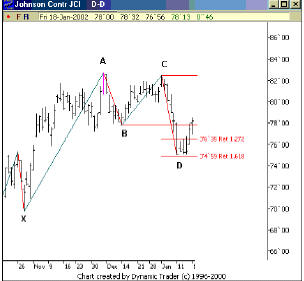
На представленном графике, мы можем видеть проекции Фибоначчи в 1.272 и 1.618, которые соотносятся с ценовым колебанием от точки B до точки C. Обратите внимание, как ценовое движение почти останавливается на уровне 1.618.
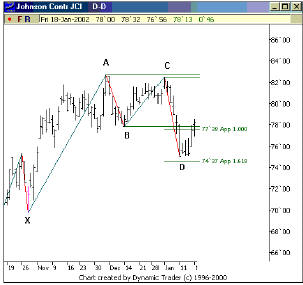
Последняя характеристика Фибоначчи, которую мы рассмотрим, как ценовое движение от точки А до точки B соотносится с ценовым движением от точки C до точки D. На графике выше мы измерили движение от точки А до точки B и спроектировали уровни в 1.00 и 1.618 этого значения от точки C. Здесь мы можем видеть, что ценовое движение сделало определенный поворот между этими двумя спроектированными уровнями.
Заключительное проектирование
Последний шаг, который желательно выполнить в любом анализе Фибоначчи, состоит в сравнении различных восстановлений и проекций от разных ценовых колебаний в анализируемой структуре. Это придает уверенность в сделанном анализе. На приведенном графике, мы имеем три проекции для точки D, которые мы рассмотрели выше. Мы сохранили ту же самую цветную схему, как и в предыдущих примерах так, чтобы можно было соотнести красные, зеленые и синие линии с предыдущими графиками. Я считаю, что важность данного графика состоит в том, что вся эта группа соотношений расположена так близко друг к другу, что вы можете различать их только по примечаниям. Это означает, что все соотношения Фибоначчи, которые проектируютсяиз различных областей структуры, подходят к тому же самому уровню, где мы можем ожидать формирование точки D. Точка D является тем самым уровнем, где мы могли бы войти в рынок с открытием бычьей позиции.
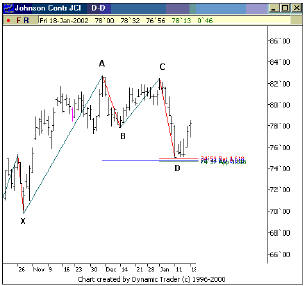
Хотя примеры, которые были приведены выше, относятся к бычьей модели Бабочки Гартли, точный обратный вариант будет верным для медвежьей модели. Все, что необходимо было бы сделать - так это перевернуть пример на первой схеме 1, чтобы получить медвежью модель изображенную выше.
Бабочка Гартли является еще одним способом, которым мы можем использовать соотношения Фибоначчи, чтобы измерить графические модели.
В последующих выпусках журнала будут рассмотрены другие разновидности модели Бабочки Гартли..
www.optionetics.com









